（Ⅰ）f'（x）=（2x-a）e^x+（x²-ax-a）e^x=（x+2）（x-a）e^x．

当a=1时，f'（0）=-2，f（0）=-1，

所以曲线y=f（x）在点（0，f（0））处的切线方程为y-（-1）=-2x，

即2x+y+1=0．

（Ⅱ）令f'（x）=0，解得x=-2或x=a．

①a≥2，则当x∈（-2，2）时，f'（x）＜0，函数f（x）在（-2，2）上单调递减，

所以，当x=2时，函数f（x）取得最小值，最小值为f（2）=（4-3a）e²．

②-2＜a＜2，则当x∈（-2，2）时，

当x变化时，f'（x），f（x）的变化情况如下表：

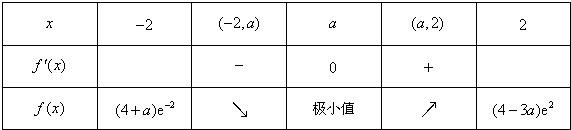
所以，当x=a时，函数f（x）取得最小值，最小值为f（a）=-a•e^a．

③a≤-2，则当x∈（-2，2）时，f'（x）＞0，函数f（x）在（-2，2）上单调递增，

所以，当x=-2时，函数f（x）取得最小值，最小值为f（-2）=（4+a）e^-2．

综上，当a≤-2时，f（x）的最小值为（4+a）e^-2；当-2＜a＜2时，f（x）的最小值为-a•e^a；

当a≥2时，f（x）的最小值为（4-3a）e²．