问题
解答题
已知函数f（x）=x3+2x2﹣ax，对于任意实数x恒有f'（x）≥2x2+2x﹣4，
（1）求实数a的取值范围；
（2）当a最大时，关于x的方程f（x）=k|x|恰有两个不同的根，求实数k的取值范围．
答案
解：（1）求导函数得：f'（x）=3x2+4x﹣a，
对于任意实数x恒有f'（x）≥2x2+2x﹣4，
即3x2+4x﹣a≥2x2+2x﹣4在R上恒成立，
即x2+2x﹣a+4≥0在R上恒成立，
∴△=4+4a﹣16≤0
∴a≤3．
（2）当a=3时，f（x）=x3+2x2﹣3x=x（x+3）（x﹣1），
关于x的方程f（x）=k|x|为x（x+3）（x﹣1）=k|x|
易知其中一个根必然是x=0，
所以当x=0时方程有一个根．
要使关于x的方程f（x）=k|x|恰有两个不同的根，
只需要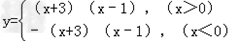
与y=k有一个交点
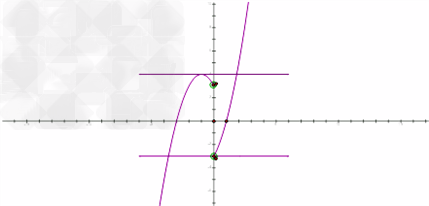
由图可得k的取值范围为k＞4，或k＜﹣3．
缺失，余留牙健康，如制作可摘局部义齿。基牙应选择（）