问题
解答题
已知函数f（x）=（ax2﹣2x+1）·e﹣x（a∈R，e为自然对数的底数）．
（I） 当时，求函数f（x）的极值；
（Ⅱ） 若函数f（x）在[﹣1，1]上单调递减，求a的取值范围．
答案
解：（ I）当a=1时，f（x）=（x2﹣2x+1）●e﹣x，
f'（x）=（2x﹣2）●e﹣x﹣（x2﹣2x+1）●e﹣x=﹣（x﹣1）（x﹣3）●e﹣x
当x变化时，f（x），f'（x）的变化情况如下表：
（ II）f'（x）=（2ax﹣2）●e﹣x﹣（ax2﹣2x+1）●e﹣x=﹣e﹣x[ax2﹣2ax﹣2x+3]
令g（x）=ax2﹣2（a+1）x+3
①若a=0，则g（x）=﹣2x+3，在（﹣1，1）内，g（x）＞0，
即f'（x）＜0，函数f（x）在区间[﹣1，1]上单调递减．
②若a＞0，则g（x）=ax2﹣2（a+1）x+3，其图象是开口向上的抛物线，
对称轴为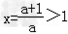
，
当且仅当g（1）≥0，即0＜a≤1时，在（﹣1，1）内g（x）＞0，f'（x）＜0，
函数f（x）在区间[﹣1，1]上单调递减．
③若a＜0，则g（x）=ax2﹣2（a+1）x+3，其图象是开口向下的抛物线，
当且仅当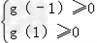
，即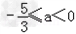
时，在（﹣1，1）内g（x）＞0，f'（x）＜0，
函数f（x）在区间[﹣1，1]上单调递减．
综上所述，函数f（x）在区间[﹣1，1]上单调递减时，a的取值范围是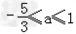
．