问题
解答题
定义函数fn(x)=(1+x)n-1,x>-2,n∈N。
(1)求证:fn(x)≥nx;
(2)是否存在区间[a,0](a<0),使函数在区间[a,0]上的值域为[ka,0]?若存在,求出最小的k值及相应的区间[a,0],若不存在,说明理由。
答案
解:(1)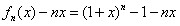
令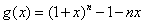
则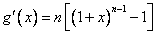
当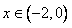 时,
时,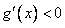
当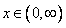 时,
时,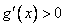
∴g(x)在x=0处取得极小值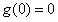 ,同时g(x)是单峰函数,则g(0)也是最小值
,同时g(x)是单峰函数,则g(0)也是最小值
∴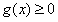
即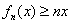 (当且仅当x=0时取等号);
(当且仅当x=0时取等号);
(2)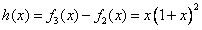
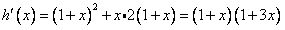
令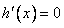 得
得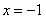 ,
,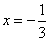
∴当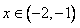 时,
时,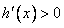
当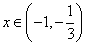 时,
时,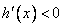
当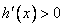
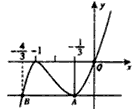
故h(x)的草图如图所示
①在 时,
时,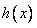 最小值
最小值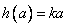
∴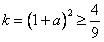
②在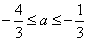 时,
时,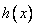 最小值
最小值
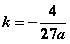 ,
,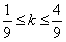
③在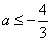 时,
时,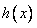 最小值=
最小值=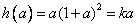
∴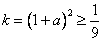 ,
,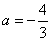 时取等号
时取等号
综上讨论可知k的最小值为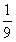 ,此时
,此时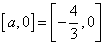 。
。