已知函数f(x)=x3-x2+ax+b(a,b∈R)的一个极值点为x=1,方程ax2+x+b=0的两个实根为α,β(α<β),函数f(x)在区间[α,β]上是单调的,
(Ⅰ)求a的值和b的取值范围;
(Ⅱ)若x1,x2∈[α,β],证明:|f(x1)-f(x2)|≤1。
(Ⅰ)解:∵f(x)=x3-x2+ax+b,
∴f′(x)=3x2-2x+a,
∵f(x)=x3-x2+ax+b的一个极值点为x=1,
∴ f′(1)=3×12-2×1+a=0,∴a=-1,
∴f′(x)=3x2-2x-1=(3x+1)(x-1),
当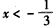 时,
时,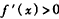 ;当
;当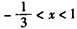 时,
时,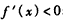 ;当x>1时,
;当x>1时,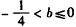 ;
;
∴函数f(x)在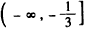 上单调递增,在
上单调递增,在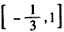 上单调递减,在
上单调递减,在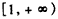 上单调递增,
上单调递增,
∵方程ax2+x+b=0的两个实根为α,β,即x2-x-b=0的两根为α,β(α<β),
∴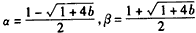 ,
,
∴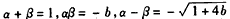 ,
,
∵函数f(x)在区间[α,β] 上是单调的,
∴区间[α,β]只能是区间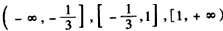 之一的子区间,
之一的子区间,
由于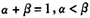 ,故
,故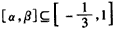 ,
,
若α<0,则α+β<1,与α+β=1矛盾;
∴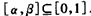 ,
,
∴方程x2-x-b=0的两根为α,β都在区间[0,1]上,
令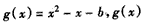 的对称轴为
的对称轴为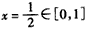 ,
,
则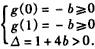 ,解得:
,解得: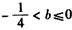 ,
,
∴实数b的取值范围是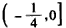 。
。
(Ⅱ)证明:由(Ⅰ)可知函数f(x)在区间[α,[α,β]]上单调递减,
∴函数f(x)在区间[α,β]上的最大值为f(α),最小值为f(β),
∵x1,x2∈[α,β],
∴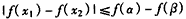
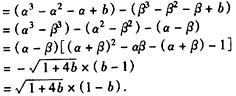
令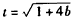 ,则
,则 ,
,
 ,
,
设 ,则
,则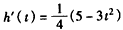 ,
,
∵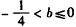 ,
,
∴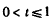 ,
,
∴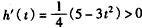 ,
,
∴函数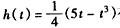 在(0,1]上单调递增,
在(0,1]上单调递增,
∴h(t)≤h(1)=1,
∴|f(x1)-f(x2)|≤1。
