问题
解答题
已知函数f(x)=x3-3ax-1,a≠0。
(1)求f(x)的单调区间;
(2)若f(x)在x=-1处取得极值,直线y=m与y=f(x)的图象有三个不同的交点,求m的取值范围。
答案
解:(1)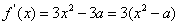
当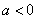 时,对
时,对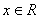 ,有
,有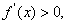
当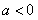 时,
时,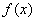 的单调增区间为
的单调增区间为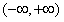
当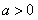 时,由
时,由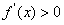 解得
解得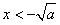 或
或 ;
;
由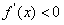 解得
解得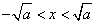 ,
,
∴当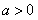 时,
时,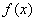 的单调增区间为
的单调增区间为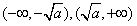 ;
;
f(x)的单调减区间为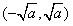 。
。
(2)∵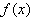 在
在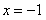 处取得极大值,
处取得极大值,
∴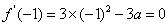
∴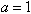
∴
由 解得
解得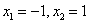 。
。
由(1)中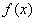 的单调性可知,
的单调性可知, 在
在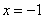 处取得极大值
处取得极大值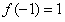 ,
,
在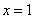 处取得极小值
处取得极小值 。
。
直线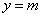 与函数
与函数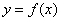 的图象有三个不同的交点,
的图象有三个不同的交点,
又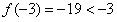 ,
,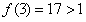 ,
,
结合f(x)的单调性可知,m的取值范围是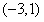 。
。
