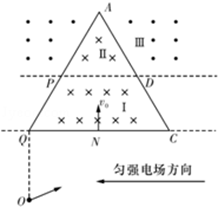
（20分）如图所示，水平线QC下方是水平向左的匀强电场；区域Ⅰ（梯形PQCD）内有垂直纸面向里的匀强磁场，磁感应强度为B；区域Ⅱ（三角形APD）内也有垂直纸面向里的匀强磁场，但是磁感应强度大小可以与区域Ⅰ不同；区域Ⅲ（虚线PD之上、三角形APD以外）有垂直纸面向外的匀强磁场，磁感应强度与区域Ⅱ内磁感应大小相等。三角形AQC是边长为2L的等边三角形，P、D分别为AQ、AC的中点．带正电的粒子从Q点正下方、距离Q点为L的O点以某一速度射出，在电场力作用下从QC边中点N以速度v0垂直QC射入区域Ⅰ，接着从P点垂直AQ射入区域Ⅲ。若区域Ⅱ、Ⅲ的磁感应强度大小与区域Ⅰ的磁感应强度满足一定的关系，此后带电粒子又经历一系列运动后又会以原速率返回O点．（粒子重力忽略不计）求：
（1）该粒子的比荷；
（2）粒子从O点出发再回到O点的整个运动过程所有可能经历的时间．
（1）该粒子的比荷为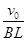
；（2）粒子从O点出发再回到O点的整个运动过程所需时间为
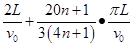（n=0，1，2…）或
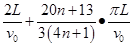（n=0，1，2…）
题目分析：（1）根据牛顿第二定律和洛仑兹力表达式有
qv0B=m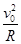
（2分）
根据题意分析带电粒子若在P点之前离开区域Ⅰ，则带电粒子不可能原速率返回，故R=L，
解得
（2分）
(2)粒子在电磁场中运动的总时间包括三段：电场中往返的时间t0、区域Ⅰ中的时间t1、区域Ⅱ和Ⅲ中的时间t2+t3．
根据平抛运动规律有
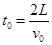（2分）
设在区域Ⅰ中的时间为t1，则
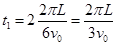（2分）
若粒子在区域Ⅱ和Ⅲ内的运动如图甲所示，则总路程为（2n+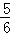
）个圆周，根据几何关系有
AP=（4nr+r）=L 解得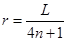
其中n=0，1，2… （3分）
区域Ⅱ和Ⅲ内总路程为 s=（2n+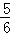）×2πr （ n=0，1，2…）
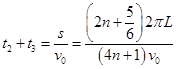（ n=0，1，2…）
总时间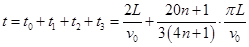
（ n=0，1，2…） （3分）
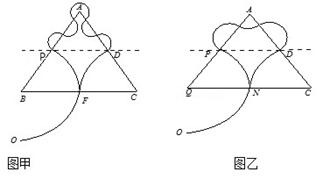
若粒子在区域Ⅱ和Ⅲ内运动如图乙所示，则总路程为（2n+1+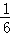
）个圆周，根据几何关系有：
AP=（4nr+3r）=L 其中n=0，1，2…
解得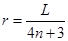 
（n=0，1，2…） （3分）
区域Ⅱ和Ⅲ内总路程为 s=（2n+1+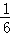）×2πr=
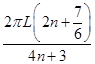（n=0，1，2…）
总时间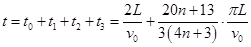
（n=0，1，2…） （3分）