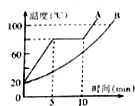
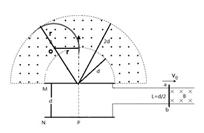
如右图甲所示,间距为d的平行金属板MN与一对光滑的平行导轨相连,平行导轨间距L=d/2,一根导体棒ab以一定的初速度向右匀速运动,棒的右侧存在一个垂直纸面向里,大小为B的匀强磁场。棒进入磁场的同时,粒子源P释放一个初速度为0的带电粒子,已知带电粒子质量为m,电量为q.粒子能从N板加速到M板,并从M板上的一个小孔穿出。在板的上方,有一个环形区域内存在大小也为B,垂直纸面向外的匀强磁场。已知外圆半径为2d, 里圆半径为d.两圆的圆心与小孔重合(粒子重力不计)

(1)判断带电粒子的正负,并求当ab棒的速度为v0时,粒子到达M板的速度v;
(2)若要求粒子不能从外圆边界飞出,则v0的取值范围是多少?
(3)若棒ab的速度v0只能是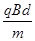 ,则为使粒子不从外圆飞出,则可以控制导轨区域磁场的宽度S(如图乙所示),那该磁场宽度S应控制在多少范围内
,则为使粒子不从外圆飞出,则可以控制导轨区域磁场的宽度S(如图乙所示),那该磁场宽度S应控制在多少范围内
(1) 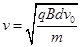 (2)
(2) 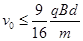 (3)
(3) 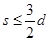
题目分析:(1)根据右手定则知,a端为正极,故带电粒子必须带负电(1分)
ab棒切割磁感线,产生的电动势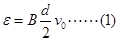 ①(2分)
①(2分)
对于粒子,据动能定理: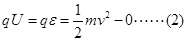 ②(2分)
②(2分)
联立①②两式,可得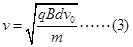 ③(1分)
③(1分)
(2)要使粒子不从外边界飞出,则粒子最大半径时的轨迹与外圆相切
根据几何关系: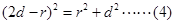 ④ 即
④ 即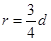 (2分)
(2分)
而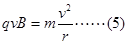 ⑤(2分)
⑤(2分)
联立③④⑤可得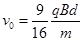 (1分)
(1分)
故ab棒的速度范围: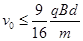 (1分)
(1分)
(3)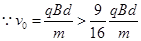 ,故如果让粒子在MN间一直加速,则必然会从外圆飞出,所以如果
,故如果让粒子在MN间一直加速,则必然会从外圆飞出,所以如果
能够让粒子在MN间只加速一部分距离,再匀速走完剩下的距离,就可以让粒子的速度变小
了。 (1分)
设磁场宽度为S0时粒子恰好不会从外圆飞出,此情况下
由④⑤可得粒子射出金属板的速度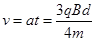 ……⑥ (2)
……⑥ (2)
粒子的加速度: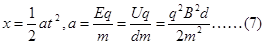 ⑦(1分)
⑦(1分)
解得:
对于棒ab:S0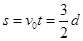 (1分)
(1分)
故磁场的宽度应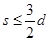 (1分)
(1分)