问题
计算题
如图，直角坐标系在一真空区域里，y轴的左方有一匀强电场，场强方向跟y轴负方向成θ=30°角，y轴右方有一垂直于坐标系平面的匀强磁场，在x轴上的A点有一质子发射器，它向x轴的正方向发射速度大小为v=2.0×106m/s的质子，质子经磁场在y轴的P点射出磁场，射出方向恰垂直于电场的方向，质子在电场中经过一段时间，运动到x轴的Q点。已知A点与原点O的距离为10cm，Q点与原点O的距离为(20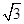
-10)cm，质子的比荷为
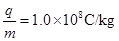。求：
（1）磁感应强度的大小和方向；
（2）质子在磁场中运动的时间；
（3）电场强度的大小。
答案
（1）
，方向垂直纸面向里 （2）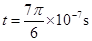
（3）
题目分析：（1）设质子在磁场中做圆运动的半径为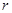
。
过A、P点分别作速度v的垂线，交点即为质子在磁场中作圆周运动的圆心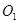
。由几何关系得
， 所以：
。（2分）
设磁感应强度为B，根据质子的运动方向和左手定则，可判断磁感应强度的方向为垂直于纸面向里。（1分）
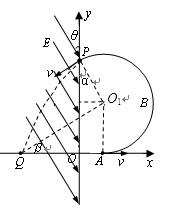
根据： 
（2分）
（2）设质子在磁场中运动的时间为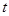
，如图所示，质子在磁场中转过
的圆周角为
，设质子在磁场中运动的周期为
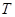
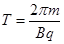（2分）
（2分）
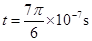（2分）（或3.66×10－7s）
（3）如图所示，质子进入电场后做类平抛运动。连接 
，由数学知识可知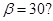
，所以，QO1垂直电场，由图可知，等效为类平抛运动的水平距离，
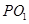为垂直距离。则有：
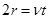
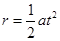
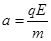（对1式2分，对2式4分，对3式５分。）
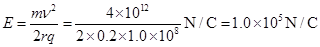(2分)