(18分)如图所示,位于A板附近的放射源P连续释放出质量分别为m和2m、电荷量均为+q的a、b两种粒子,它们从静止开始经极板A、B间电场加速后,沿中心轴线方向进入平行极板M、N间的偏转电场,飞出偏转电场后进入右侧的有界匀强磁场,最后打在位于磁场边界上的荧光屏上并产生光斑(荧光屏的下端位于中心轴线上).已知A、B问电压为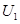 ;极板M、N长为L,间距为
;极板M、N长为L,间距为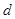 ,也板间电压为
,也板间电压为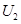 ,磁场的磁感应强度大小为B、方向垂直纸面向里,磁场的左边界与中心轴线垂直.不计粒子的重力及其相互间的作用.求
,磁场的磁感应强度大小为B、方向垂直纸面向里,磁场的左边界与中心轴线垂直.不计粒子的重力及其相互间的作用.求
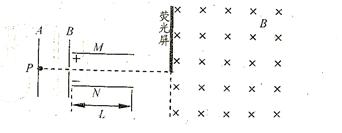
(1)两种粒子射入偏转电场时的初速度;
(2)两种粒子离开偏转电场时的偏转距离和偏转角度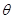 的正切值;
的正切值;
(3)实验发现,荧光屏上出现了两个光斑,求这两个光斑间的距离.
(1)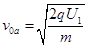 ,
,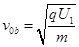 (2)
(2)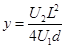 ,
,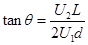 (3)
(3)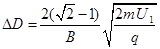
题目分析:(1)设a、b粒子射入偏转电场时的初速度分别为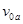 和
和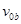 ,有
,有
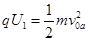 (1分)
(1分)
解得: 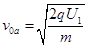 (1分)
(1分)
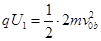 (1分)
(1分)
解得: 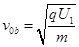 (1分)
(1分)
(2)设a粒子在偏转电场中的骗局为y,偏角为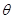 ,有
,有
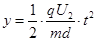 (2分)
(2分)
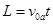 (1分)
(1分)
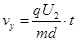 (1分)
(1分)
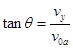 (1分)
(1分)
解得: 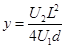 (1分)
(1分)
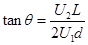 (1分)
(1分)
可见偏距和偏角与粒子本身无关,两种粒子偏距和偏角相同.
(3)对a粒子,射出偏转电场时,设速度为va,有
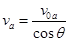 (1分)
(1分)
粒子射入磁场后,有
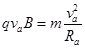 (2分)
(2分)
由几何关系得,粒子在磁场中的射入点与其光斑间的距离为
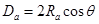 (1分)
(1分)
解得: 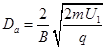 (1分)
(1分)
同理可得b粒子在磁场中的射入点与其光斑间的距离为
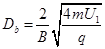 (1分)
(1分)
两个光斑间的距离为 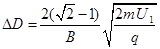 (1分)
(1分)
说明:求粒子在磁场中半径时,要列出原始公式,直接使用半径公式,该得分点得1分。
