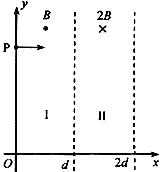
(19分)如图,在区域I(0≤x≤d)和区域II(d≤x≤2d)内分别存在匀强磁场,磁感应强度大小分别为B和2B,方向相反,且都垂直于Oxy平面。一质量为m、带电荷量q(q>0)的粒子a于某时刻从y轴上的P点射入区域I,其速度方向沿x轴正向。已知a在离开区域I时,速度方向与x轴正方向的夹角为30°;此时,另一质量和电荷量均与a相同的粒子b也从p点沿x轴正向射入区域I,其速度大小是a的1/3。不计重力和两粒子之间的相互作用力。求
(1)粒子a射入区域I时速度的大小;
(2)当a离开区域II时,a、b两粒子的y坐标之差。
(1) (2)
(2)
题目分析:(1)设粒子a在I内做匀速圆周运动的圆心为C(在y轴上),半径为Ra1,粒子速率为va,运动轨迹与两磁场区域边界的交点为 ,如图。由洛仑兹力公式和牛顿第二定律得
,如图。由洛仑兹力公式和牛顿第二定律得
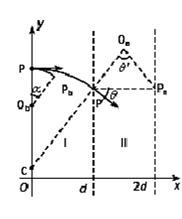
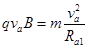 (1)
(1)
由几何关系得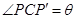 (2)
(2)
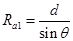 (3)
(3)
式中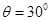
由(1)(2)(3)式得
 (4)
(4)
(2)设粒子在II区内做圆周运动的的圆心为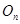 ,半径为
,半径为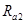 ,射出点为
,射出点为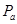 (图中末画出轨迹)
(图中末画出轨迹)
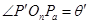
由洛仑兹力分式和牛顿第二定律得
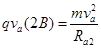 (5)
(5)
由(1)(5)式得: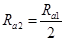 (6)
(6)
C,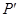 和
和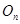 三点共线,且由(6)式知
三点共线,且由(6)式知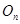 必位于
必位于
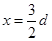 (7)
(7)
的平面上,由对称性知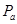
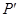 纵坐标相同,即
纵坐标相同,即
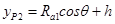 (8)
(8)
式中h是C点的Y坐标
设b在I中运动的轨道半径为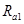 ,由洛仑兹力公式和牛顿第二定律得
,由洛仑兹力公式和牛顿第二定律得
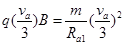 (9)
(9)
设a到达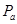 点时,b位于
点时,b位于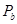 点,转过的角度为α。如果b没有飞出I,则
点,转过的角度为α。如果b没有飞出I,则
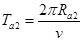 (10)
(10)
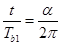 (11)
(11)
式中,t是a在区域II中运动的时间,而
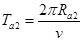 (12)
(12)
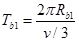 (13)
(13)
由⑤⑨⑩(11)(12)(13)式得
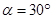 (14)
(14)
由①③⑨(14)式可见,b没有飞出I。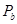 点的y坐标为
点的y坐标为
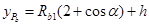 (15)
(15)
由(1)(3)(8)(9)(14)(15)式及题给条件得,a、b两粒子的y坐标之差为
 (16)
(16)
