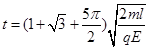问题
计算题
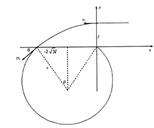
(16分)如图所示，直角坐标系xoy的第一象限内有场强为E方向沿x轴负向的匀强电场，第二象限内有方向沿y轴负向的匀强电场，在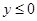
的区域内有方向垂直坐标平面的匀强磁场．一质量为m、电荷量为q的正粒子(不计重力)，从P(
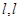)点由静止开始运动， 通过第二象限后经
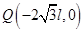点再进入y≤0区域，并恰好经过坐标原点O.求
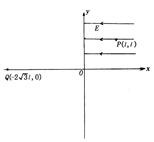
(1)第二象限内匀强电场的场强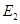
．
(2)y≤0区域内匀强磁场的磁感应强度B．
(3)粒子从P到0经历的时间．
答案
(1) 
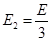(2) 
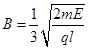(3) 
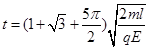
题目分析：(1)粒子在第一象限内做匀加速直线运动
所以根据动能定理可得：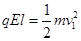
在第二象限内做匀变速曲线运动，即类平抛运动，故有：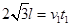
, 
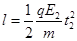
整理可得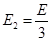
(2)设粒子经过Q点时速度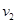
与负向的夹角为
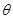，则根据动能定理可得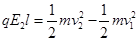
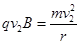，故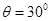
粒子在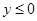
区域内做匀速圆周运动，所以根据几何知识可得：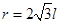
根据牛顿第二定律可得：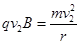
整理可得：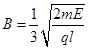
(3)粒子在各区域内的运动时间分别满足：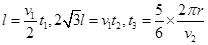
从P到O的时间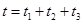
，
解得：
