问题
计算题
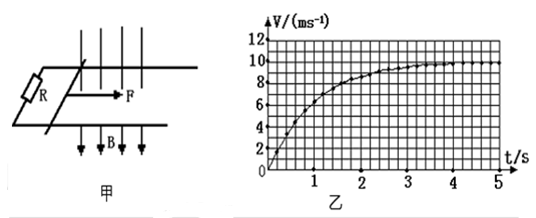
（12分）如图甲所示，放置在水平桌面上的两条光滑导轨间的距离L=1m，质量m=1kg的光滑导体棒放在导轨上，导轨左端与阻值R=4Ω的电阻相连，导体棒及导轨的电阻不计，所在位置有磁感应强度为B=2T的匀强磁场，磁场的方向垂直导轨平面向下。现在给导体棒施加一个水平向右的恒定拉力F，并每隔0.2s测量一次导体棒的速度，乙图是根据所测数据描绘出导体棒的v-t图象。设导轨足够长，求：
（1）力F的大小；
（2）t =1.2s时，导体棒的加速度；
（3）估算1.6s内电阻R上产生的热量。
答案
（1）10N （2）3m/s2 （3）48J
题目分析：（1）由图可知，导体棒运动的速度达到10m/s时开始做匀速运动，此时安培力和拉力F大小相等。导体棒匀速运动的速度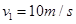
匀速运动后导体棒上的电动势：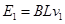
(1分)
导体棒受的安培力：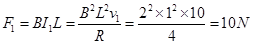
(2分)
则：
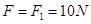(1分)
（2）由图可知，时间t=1.2s时导体棒的速度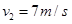
此时导体棒上的电动势：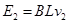
(1分)
导体棒受的安培力：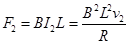
＝
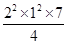N＝7N (2分)
由牛顿定律得：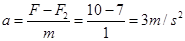
(1分)
（3）由图知，到1.6s处，图线下方小方格的个数为40个，每个小方格代表的位移为
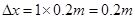
所以1.6s内导体棒的位移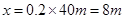 
(2分)
拉力F做功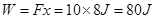 
(1分)
由图知此时导体棒的速度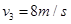 
导体棒动能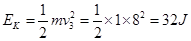 
根据能量守恒定律，产生的热量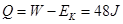
(1分)
（说明：格数为39~42均正确 ，答案范围46 ~52J ）