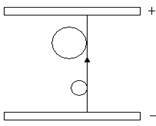
(18分)如图甲所示,两块足够大的平行金属板水平放置,极板间加有空间分布均匀、大小随时间周期性变化、方向竖直向下的电场,变化规律如图乙所示,在t=0时刻从负极板由静止释放一个质量为m、带电量为q(q<0)的质点。已知电场强度 ,同时t0也为已知量。
,同时t0也为已知量。
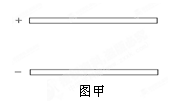

(1)若质点恰好在t=3t0时刻到达正极板,试求两极板之间的距离d
(2)在第(1)问的条件下,在极板间再加上空间分布均匀、大小随时间周期性变化、方向垂直纸面向外的磁场,变化规律如图丙所示,已知磁感应强度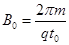 。试求:
。试求:
①带电质点经过多长时间到达正极板
②带电质点在极板间做圆周运动的最大半径
③画出质点在极板间运动的轨迹图(不需要写计算过程)
(1)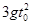 (2)①
(2)① 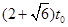 ②
② 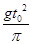 ③ 见下图
③ 见下图
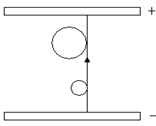
题目分析:(1)质点在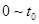 时间内,
时间内,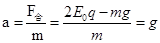 ,做初速度为0的匀加速直线运动
,做初速度为0的匀加速直线运动
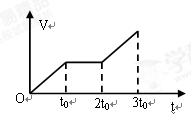
在t0~2t0时间内,受力平衡,做匀速直线运动,在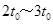 时间内,再做加速度为g的匀加速直线运动,v—t图像如图.
时间内,再做加速度为g的匀加速直线运动,v—t图像如图.
有: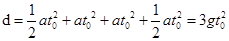 (4分)
(4分)
(2)①带电质点在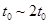 时间和
时间和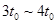 时间内,所受重力和电场力平衡,洛伦兹力提供向心力,做匀速圆周运动,其他时间没有磁场,与上问相同以
时间内,所受重力和电场力平衡,洛伦兹力提供向心力,做匀速圆周运动,其他时间没有磁场,与上问相同以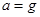 做匀加速直线运动
做匀加速直线运动
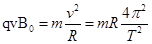 (1分)
(1分)
所以有: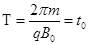 (1分)
(1分)
带电质点在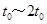 时间和
时间和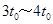 时间内将完成两个圆周,即水平方向没有位移,且速度不变,接着原来的匀加速直线运动继续
时间内将完成两个圆周,即水平方向没有位移,且速度不变,接着原来的匀加速直线运动继续
带电质点做匀加速直线运动到达正极板时有
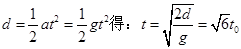 (2分)
(2分)
由于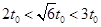 ,所以质点在
,所以质点在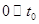 做匀加速直线运动,
做匀加速直线运动,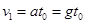 ,
, 
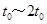 匀速圆周运动回到
匀速圆周运动回到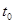 时刻的速度和位置。此时圆周运动半径
时刻的速度和位置。此时圆周运动半径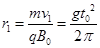 ,位移为距离下极板最远的位移
,位移为距离下极板最远的位移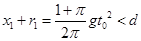 ,所以没有到达上极板
,所以没有到达上极板
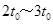 继续匀加速直线运动,速度变为
继续匀加速直线运动,速度变为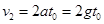 ,位移
,位移
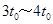 时间继续圆周运动而且
时间继续圆周运动而且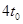 回到
回到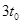 时的位置和速度,此过程,圆周运动半径
时的位置和速度,此过程,圆周运动半径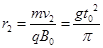
位移为距离下极板最远的位移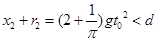 仍没有到达上极板
仍没有到达上极板
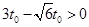 所以继续匀加速运动刚好满足加速时间
所以继续匀加速运动刚好满足加速时间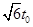 ,到达上极板。
,到达上极板。
所以到达正极板的总时间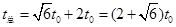 (2分)
(2分)
②根据上问分析一共经过了2个圆周运动,圆周运动半径最大的是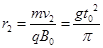 (4分)
(4分)
③如图 ,运动轨迹为两个圆周和直线段。