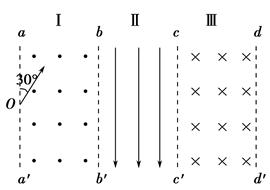
如图所示,aa′、bb′、cc′、dd′为区域Ⅰ、Ⅱ、Ⅲ的竖直边界,三个区域的宽度相同,长度足够大,区域Ⅰ、Ⅲ内分别存在垂直纸面向外和向里的匀强磁场,区域Ⅱ存在竖直向下的匀强电场.一群速率不同的带正电的某种粒子,从边界aa′上的O处,沿着与Oa成30°角的方向射入Ⅰ区.速率小于某一值的粒子在Ⅰ区内运动时间均为t0;速率为v0的粒子在Ⅰ区运动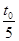 后进入Ⅱ区.已知Ⅰ区的磁感应强度的大小为B,Ⅱ区的电场强度大小为2Bv0,不计粒子重力.求:
后进入Ⅱ区.已知Ⅰ区的磁感应强度的大小为B,Ⅱ区的电场强度大小为2Bv0,不计粒子重力.求:
(1)该种粒子的比荷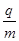 ;
;
(2)区域Ⅰ的宽度d;
(3)速率为v0的粒子在Ⅱ区内运动的初、末位置间的电势差U;
(4)要使速率为v0的粒子进入Ⅲ区后能返回到Ⅰ区,Ⅲ区的磁感应强度B′的大小范围应为多少?
(1)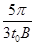 (2)
(2)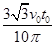 (3)
(3)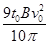 (4)B′≥
(4)B′≥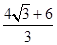 B
B
(1)速率小于某一值的粒子在区域Ⅰ中运动时间均为t0,这些粒子不能从bb′离开区域Ⅰ,其轨迹如图a所示(图中只画出某一速率粒子的轨迹).粒子运动轨迹的圆心角为φ1=300°①
t0=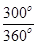 T=
T=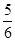 T②
T②
由牛顿第二定律得qvB=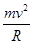 ③
③
T= ④
④
得粒子的比荷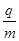 =
=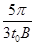 ⑤
⑤

(2)设速率为v0的粒子在区域Ⅰ内运动轨迹所对圆心角为φ2,φ2=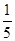 φ1=60°⑥
φ1=60°⑥
由几何知识可知,穿出bb′时速度方向与bb′垂直,其轨迹如图b所示,设轨迹半径为R0,d=R0sin φ2⑦
R0=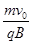
区域Ⅰ的宽度d=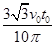 ⑧
⑧
(3)设速率为v0的粒子离开区域Ⅱ时的速度大小为v1,方向与边界cc′的夹角为φ3
水平方向有d=v0t 竖直方向有vy=at⑨
a=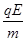 =
=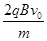 ⑩
⑩
tan φ3=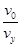 ⑪
⑪
v1=2v0⑫
φ3=30°⑬
由动能定理得qU=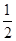 mv
mv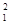 -
-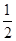 mv
mv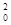 ⑭
⑭
U=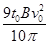 ⑮
⑮
(4)速率为v0的粒子在区域Ⅲ内做圆周运动,当Ⅲ区内的磁感应强度为B1时,粒子恰好不能从区域Ⅲ的边界dd′飞出,设其轨迹半径为r,则r(1+cos φ3)=d⑯
r=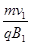 ,解得B1=
,解得B1=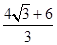 B⑰
B⑰
所以,粒子能返回Ⅰ区,B′的大小范围为B′≥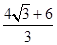 B⑱
B⑱
