问题
计算题
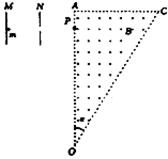
如图所示，直角三角形OAC（α= 30˚）区域内有B = 0.5T的匀强磁场，方向如图所示。两平行极板M、N接在电压为U的直流电源上，左板为高电势。一带正电的粒子从靠近M板由静止开始加速，从N板的小孔射出电场后，垂直OA的方向从P点进入磁场中。带电粒子的荷质比为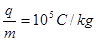
，OP间距离为l＝0.3m。全过程不计粒子所受的重力，求：
（1）要使粒子从OA边离开磁场，加速电压U需满足什么条件?
（2）粒子分别从OA、OC边离开磁场时，粒子在磁场中运动的时间。
答案
（1）若加速电压U0＝125 V，U<U0，则r<R，粒子从OA边射出；
（2）2π×10－5s;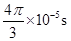
．
题目分析：（1）如图所示，当带电粒子的轨迹与OC边相切时为临界状态，设临界半径为R，加速电压U0，则有：
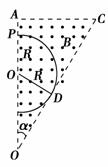
R＋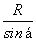
＝L，解得R＝0.1 m
qU0＝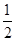
mv2，qvB＝m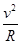
得U0＝125 V，U<U0，则r<R，粒子从OA边射出．
（2）带电粒子在磁场做圆周运动的周期为T＝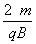
＝4π×10－5s
当粒子从OA边射出时，粒子在磁场中恰好运动了半个周期
t1＝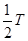
＝2π×10－5s
当粒子从OC边射出时，粒子在磁场中运动的时间小于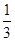
周期，
即t2≤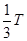
＝
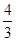×10－5s.