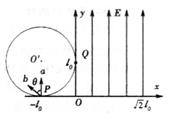
(18分)如图所示,在xOy坐标系第二象限内有一圆形匀强磁场区域,半径为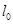 ,圆心O′坐标为(-
,圆心O′坐标为(-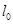 ,
, 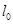 ),磁场方向垂直xOy平面。在x轴上有坐标(-
),磁场方向垂直xOy平面。在x轴上有坐标(- 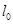 ,0)的P点,两个电子a、b以相同的速率v沿不同方向从P点同时射入磁场,电子
,0)的P点,两个电子a、b以相同的速率v沿不同方向从P点同时射入磁场,电子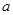 的入射方向为y轴正方向,b的入射方向与y轴正方向夹角为
的入射方向为y轴正方向,b的入射方向与y轴正方向夹角为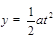 。电子a经过磁场偏转后从y轴上的 Q(0,
。电子a经过磁场偏转后从y轴上的 Q(0,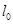 )点进入第一象限,在第一象限内紧邻y轴有沿y轴正方向的匀强电场,场强大小为
)点进入第一象限,在第一象限内紧邻y轴有沿y轴正方向的匀强电场,场强大小为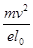 ,匀强电场宽为
,匀强电场宽为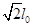 。已知电子质量为
。已知电子质量为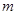 、电荷量为
、电荷量为 ,不计重力及电子间的相互作用。求:
,不计重力及电子间的相互作用。求:
(1)磁场的磁感应强度B的大小
(2)b电子在磁场中运动的时间
(3)a、b两个电子经过电场后到达x轴的坐标差Δx
(1)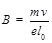 (2)
(2)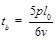 (3)
(3)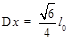
题目分析:(1) 两电子轨迹如图。
A |
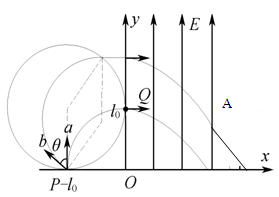 由图可知,a电子作圆周运动的半径R=
由图可知,a电子作圆周运动的半径R=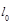 (1分)
(1分)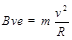 (1分)
(1分)
可得: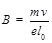 (1分)
(1分)
(2)由几何知识分析可知b电子在磁场中运动转过的圆心角为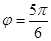 (1分)
(1分)
b电子在磁场中运动的时间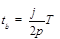 (1分)
(1分)
b电子在磁场中运动的周期为 (1分)解得
(1分)解得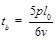 (1分)
(1分)
|
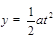 (1分)
(1分) 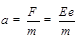 ( 1分)
( 1分) (1分)
(1分)
代入y=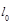 ,即a电子恰好击中x轴上坐标为
,即a电子恰好击中x轴上坐标为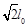 的位置 (1分)
的位置 (1分)
根据几何分析,PO´AO″为菱形,所以PO´与O″A平行.又因为PO´⊥x轴, O″A⊥x轴,所以粒子出场速度vA平行于x轴,即b电子经过磁场偏转后,也恰好沿x轴正方向进入电场, (1分)
有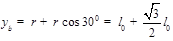 (1分)
(1分)
当b沿y方向运动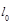 后沿与x轴方向成
后沿与x轴方向成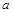 做匀速直线运动
做匀速直线运动
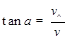 (1分)
(1分)
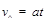 (1分)
(1分)
可得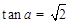 (1分)
(1分)
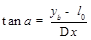 (1分)
(1分)
解得: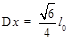 (1分)
(1分)
用其他方法解过程及结果正确的给满分,结果不准确的要尽量给步骤分。
