解：（I）当b=1时f（x）=e^x﹣x，

∴f'（x）=e^x﹣1，

令f'（x）=0，得x=0，

f'（x），f（x）随x的变化情况如下表： 

 f（x）的单调递减区间为（﹣∞，0），单调递增区间为（0，+∞）；

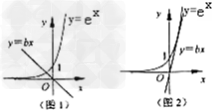
（2）转化为y=ex与y=bx的图象只有一个交点

当b＜0时，作出图象，发现满足要求；

当b≥0时，作出图象，

发现当且仅当y=e^x与y=bx相切时有一个交点

设切点为（x，y），则 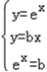，解得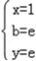 

所以，b＜0或b=e

（3）f（x）=e^x﹣bx，f'（x）=e^x﹣b，令f'（x）=e^x﹣b=0，则x=lnb

当x∈（﹣∞，lnb）时，f'（x）=ex﹣b＜0，所以f（x）递减；

当x∈（lnb，+∞）时，f'（x）=ex﹣b＞0，所以f（x）递增；

所以，f（x）的最小值为f（lnb）=b﹣blnb=b（1﹣lnb）

当0＜b≤e时，f（lnb）=b（1﹣lnb）≥0，所以f（x）=e^x﹣bx≥0

∴|f（x）|=f（x）=e^x﹣bx，

此时，|f（x）|在（﹣∞，+∞）上无极大值，所以在（0，2）上无极大值

当b＞e时，f（lnb）=b（1﹣lnb）＜0，

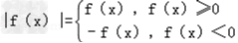∴ ，可得：

若b≥e²，则lnb≥2，此时|f（x）|在（0，2）上无极大值；

若b＜e²，则lnb＜2，此时|f（x）|在（0，2）上有极大值|f（lnb）|=b（lnb﹣1）

综上得：当0＜b≤e或b≥e²时，|f（x）|在（0，2）上无极大值；

当e＜b＜e²时，|f（x）|在（0，2）上有极大值|f（lnb）|=b（lnb﹣1）