问题
计算题
如图所示,在匀强电场中建立直角坐标系xoy,y轴竖直向上,一质量为m、电荷量为+q的微粒从x轴上的M点射出,方向与x轴夹角为θ,微粒恰能以速度v做匀速直线
运动,重力加速度为g。

(1)求匀强电场场强E的大小及方向;
(2)若再叠加一圆形边界的匀强磁场,使微粒能到达x轴上的N点,M、N两点关于原点o对称,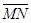 =L,微粒运动轨迹也关于y轴对称。 己知所叠加磁场的磁感应强度大小为B,方向 垂直xoy平面向外。求磁场区域的最小面积S 及微粒从M运动到N的时间t。
=L,微粒运动轨迹也关于y轴对称。 己知所叠加磁场的磁感应强度大小为B,方向 垂直xoy平面向外。求磁场区域的最小面积S 及微粒从M运动到N的时间t。
答案
(1)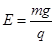 竖直向上(2)
竖直向上(2)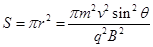
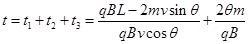
题目分析:
(1)当微粒在电场中做匀速直线运动时,它所爱的电场力与重力平衡。所以有:qE-mg=0 ①(2分)
由①式可解得: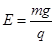 ②(1分)
②(1分)
E的方向竖直向上 (1分)
(2) 微粒在磁场中运动,由洛仑兹力和向心力公式得:
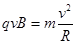 ③(2分)
③(2分)
由③式得: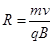 ④
④
如图所示,当PQ为圆形磁场的直径时,圆形磁场面积最小。(3分)

由几何知识可得:r=Rsinθ ⑤(2分)
其面积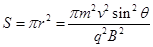 ⑥
⑥
又由圆周运动规律可得: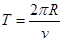 ⑦ (1分)
⑦ (1分)
根据几何关系可知偏转角为2θ,则在磁场中运动的时间:
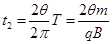 ⑧(2分)
⑧(2分)
又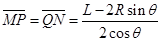 ⑨(1分)
⑨(1分)
且有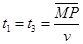 ⑩(1分)
⑩(1分)
故微粒从M运动到N的时间: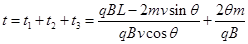 (11) (2分)
(11) (2分)
