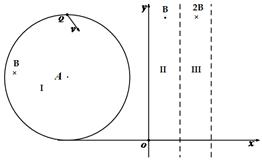
（18分）如图，在第二象限的圆形区域I存在匀强磁场，区域半径为R，磁感应强度为B，且垂直于Oxy平面向里;在第一象限的区域II和区域III内分别存在匀强磁场，磁场宽度相等，磁感应强度大小分别为B和2B，方向相反，且都垂直于Oxy平面。质量为m、带电荷量q（q＞0）的粒子a于某时刻从圆形区域I最高点Q（Q和圆心A连线与y轴平行）进入区域I，其速度v＝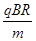
。已知a在离开圆形区域I后，从某点P进入区域II。该粒子a离开区域II时，速度方向与x轴正方向的夹角为30°；此时，另一质量和电荷量均与a相同的粒子b从P点进入区域II，其速度沿x轴正向，大小是粒子a的
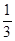。不计重力和两粒子之间的相互作用力。求：
（1）区域II的宽度；
（2）当a离开区域III时，a、b两粒子的y坐标之差.
（1）
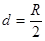（2）
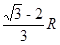
题目分析：（1）如图所示，a粒子进入区域I后，由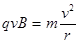
故a粒子在区域I做圆周运动的半径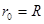
…………（1分）
其轨迹圆心为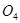
,
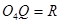且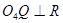
由几何知识得：
a粒子从某点D出射时，速度v沿x轴正方向. …………（2分）
a粒子从P点沿x轴正方向进入区域II后，由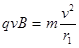
得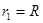
，可找到圆心
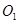…………（1分）
作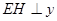
轴，由图知：
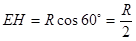，即磁场区域宽度 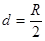…………（2分）
(2)①对a粒子的运动进行分析：
进入区域Ⅲ后，由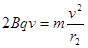
，得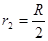
……..（1分）
连接O1E并延长，取EO2=r2，则O2为a粒子在区域Ⅲ中的轨迹圆心延长HE交Ⅲ右边界于F，连接O2F
由已知条件易证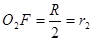
，故F点是a粒子在区域Ⅲ中的出射点
且轨迹所对应的圆心角为60o
故a粒子在区域Ⅲ中运动的时间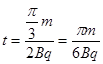
…..（1分）
由图根据几何关系知：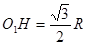
…..（1分）
②对b粒子的运动进行分析：
b粒子进入区域Ⅱ后，由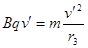
，得：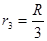
且其轨迹圆心O3位于y轴上
P点进入区域II，运动时间为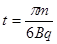
，故其轨迹所对应的圆心角为
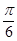…（1分）
由图根据几何知识：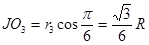
…………（1分）
综上分析可知：
当a离开区域III时，a、b两粒子的y坐标之差为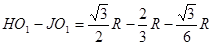
即坐标差为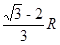 …………（2分）
