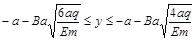问题
计算题
如图所示,在xOy平面内,紧挨着的三个“柳叶”形有界区域①②③内(含边界上)有磁感应强度为B的匀强磁场,它们的边界都是半径为a的l/4圆,每个1/4圆的端点处的切线要么与x轴平行、要么与y轴平行.①区域的下端恰在O点,①②区域在A点平滑连接、②③区域在C点平滑连接:大量质量均为m,电荷量均为q的带正电的粒子依次从坐标原点。以相同的速率、各种不同的方向射入第一象限内(含沿x’轴、y轴方向),它们只要在磁场中运动,轨道半径就都为a,在y≤—a的区域,存在场强为E的沿一x方向的匀强电场.整个装置在真空中.不计粒子重力、不计粒子之间的相互作用.求:
(1)粒子从O点出射时的速率v0;
(2)这群粒子中,从P点射出至运动到x轴上的最长时间;
(3)这群粒子到达y轴上的区域范围.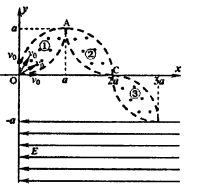
答案
(1)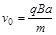 (2)
(2)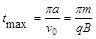 (3)
(3)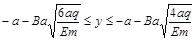
题目分析:(1)由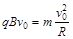 得
得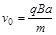
(2)这些粒子中,从O沿+y轴方向射入磁场的粒子,从O到C耗时最长

由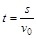 得
得 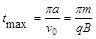
(3)这些粒子经过①区域偏转后方向都变成与 +x轴平行;接着匀速直线进入②区域,经过②区域偏转又都通过C点;
从C点进入③区域,经过③区域偏转,离开③区域时,所有粒子都变成与-y轴平行(即垂直进入电场)
对于从x = 2a进入电场的粒子,在-x方向的分运动有: 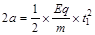
解得 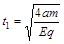
则该粒子运动到y轴上的坐标为
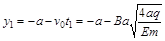
对于从x = 3a进入电场的粒子,在-x方向的分运动有: 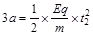
解得 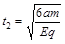
则该粒子运动到y轴上的坐标为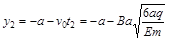
这群粒子运动到y轴上的区间为