问题
填空题
已知z1,z2∈C且|z1|=4,|z1-z2|=5,|z1+z2|=5,则|z2|=______.
答案
已知z1,z2∈C且|z1|=4,|z1-z2|=5,|z1+z2|=5,
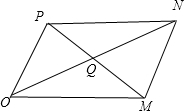
∵|z1|,|z1+z2|,|z1-z2|,|z2|四个线段组成以|z1|,|z2|为邻边,
|z1+z2|,|z1-z2|为对角线的平行四边形,设|OM|=|z2|,|OP|=|z1|,|ON|=|z1+z2|,则|MP|=|z1-z2|,
设MP∩ON=Q,在△OPQ中,由余弦定理可得 16=
+25 4
-2×25 4
×5 2
cos∠OQP,5 2
解得 cos∠OQP=-
,∴cos∠OQM=7 25
.7 25
△OQM中,由余弦定理可得 |z2|2=
+25 4
-2×25 4
×5 2
cos∠OQM=9,5 2
故|z2|=3,
故答案为 3.