问题
解答题
设a为实数,函数f(x)=x3-x2-x+a,
(Ⅰ)求f(x)的极值;
(Ⅱ)当a在什么范围内取值时,曲线y=f(x)与x轴仅有一个交点。
答案
解:(Ⅰ)令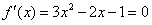 得:
得: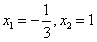 ,
,
又∵当x∈(-∞, )时,f′(x)>0;
)时,f′(x)>0;
当x∈(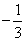 ,1)时,f′(x)<0;
,1)时,f′(x)<0;
当x∈(1,+∞)时,f′(x)>0,
∴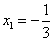 与
与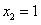 分别为f(x)的极大值与极小值点,
分别为f(x)的极大值与极小值点,
∴f(x)极大值=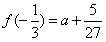 ,f(x)极小值=a-1;
,f(x)极小值=a-1;
(Ⅱ)∵f(x)在(-∞,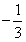 )上单调递增,
)上单调递增,
∴当x→-∞时,f(x)→-∞;
又f(x)在(1,+∞)单调递增,当x→+∞时,f(x)→+∞,
∴当f(x)极大值<0或f(x)极小值>0时,曲线f(x)与x轴仅有一个交点,
即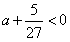 或a-1>0,
或a-1>0,
∴a∈(-∞,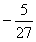 )∪(1,+∞)。
)∪(1,+∞)。
