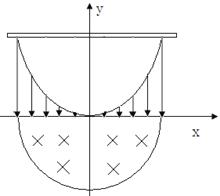
(22分)如图所示,在一二象限内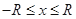 范围内有竖直向下的运强电场E,电场的上边界方程为
范围内有竖直向下的运强电场E,电场的上边界方程为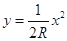 。在三四象限内存在垂直于纸面向里、边界方程为
。在三四象限内存在垂直于纸面向里、边界方程为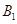 的匀强磁场。现在第二象限中电场的上边界有许多质量为m,电量为q的正离子,在
的匀强磁场。现在第二象限中电场的上边界有许多质量为m,电量为q的正离子,在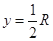 处有一荧光屏,当正离子达到荧光屏时会发光,不计重力和离子间相互作用力。
处有一荧光屏,当正离子达到荧光屏时会发光,不计重力和离子间相互作用力。
(1)求在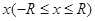 处释放的离子进入磁场时速度。
处释放的离子进入磁场时速度。
(2)若仅让横坐标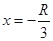 的离子释放,它最后能经过点
的离子释放,它最后能经过点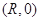 ,求从释放到经过点
,求从释放到经过点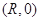 所需时间t.
所需时间t.
(3)若同时将离子由静止释放,释放后一段时间发现荧光屏上只有一点持续发出荧光。求该点坐标和磁感应强度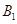 。
。
(1)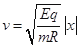 (2)
(2)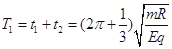 ,
,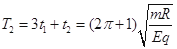 ;
;
(3)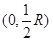
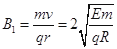
题目分析:
(1)于x处释放离子,由动能定理得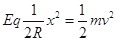 (2分)
(2分)
得离子进入磁场时的速度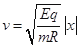 (2分)
(2分)
(2)由(1)得在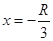 处释放的离子到达x轴时速度为
处释放的离子到达x轴时速度为
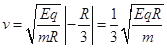 (1分)
(1分)
从释放到到达x轴时间为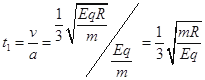 (1分)
(1分)
第一种情况:离子直接从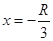 经磁场达
经磁场达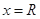 处。
处。
在磁场中经历半圆时间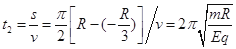 (1分)
(1分)
总时间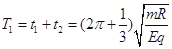 (1分)
(1分)
第二种情况:离子直接从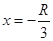 经磁场达
经磁场达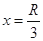 处进入电场返回磁场再到
处进入电场返回磁场再到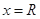 处
处
易得在磁场中时间仍然为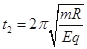 (2分)
(2分)
在电场中时间为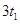
 (1分)
(1分)
总时间为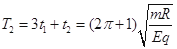 (1分)
(1分)
(3)在磁场B中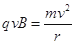 (2分)
(2分)
所以运动半径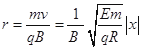 (2分)
(2分)
可以看出,B一定时,必有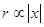 , 当
, 当 时,
时,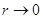 (离子经磁场偏转从逼近原点出磁场)因此,所有离子都从原点(0,0)点出磁场,击中荧光屏上
(离子经磁场偏转从逼近原点出磁场)因此,所有离子都从原点(0,0)点出磁场,击中荧光屏上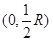 (2分)
(2分)
则有 (2分)
(2分)
因为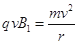 所以
所以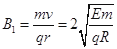 (2分)
(2分)
