问题
解答题
设x=1和x=2是函数f（x）=x5+ax3+bx+1的两个极值点，
(Ⅰ)求a、b的值；
(Ⅱ)求f（x）的单调区间。
答案
解：（Ⅰ）f′(x)=5x4+3ax2+b，
由假设知f′(1)=5+3a+b=0，f′(2)=24×5+22×3a+b=0，
解得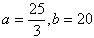
；
（Ⅱ）由（Ⅰ）知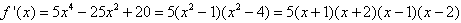
，
当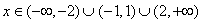
时，f′(x)＞0，
当x∈(-2，-1)∪(1，2)时，f′(x)＜0，
因此f(x)的单调增区间是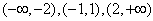
，f(x)的单调减区间是(-2，-1)，(1，2)。
