问题
解答题
（1）一幅图案，在某个顶点处由三个边长相等的正多边形镶嵌而成，其中的两个分别是正方形和正六边形，则第三个正多边形的边数是_________。
（2）从下列图中选择四个拼图板，可拼成一个矩形，正确的选择方案为_________，（填写拼图板的代码即可
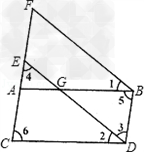
（3）已知：如图，∠1=∠2，∠3=∠4，∠5=∠6，求证：ED∥FB。
答案
解：（1）因为正方形和正六边形的内角分别是90°，120°，所以第三个正多边形的内角是150°，所以第三个正多边形的边数是12；
（2）根据矩形的判定，有三个是直角的四边形是矩形，由①②③④刚好能组成一个四个角都是直角的四边形，正确的选择方案为：①②③④；
（3）∵∠3=∠4，
∴BD∥CF，
∴∠5=∠BAF，
∵∠5=∠6，
∴∠BAF=∠6，
∴AB∥CD，
∴∠2=∠AGE，
∵∠1=∠2，
∴∠AGE=∠1，
∴ED∥FB。
是一种医药中间体，常用来制备抗凝血药，可通过下列路线合成