如图所示，位于竖直平面内的坐标系
，在其第三象限空间有沿水平方向的、垂直于纸面向外的匀强磁场，磁感应强度大小为B=0．5T，还有沿x轴负方向的匀强电场，场强大小为E=2N/C。在其第一象限空间有沿y轴负方向的、场强大小也为E的匀强电场，并在
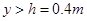的区域有磁感应强度也为B的垂直于纸面向里的匀强磁场。一个带电荷量为q的油滴从图中第三象限的P点得到一初速度，恰好能沿PO作匀速直线运动（PO与x轴负方向的夹角为
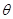=45°），并从原点O进入第一象限。已知重力加速度g=10m/s2，问：
（1）油滴在第三象限运动时受到的重力、电场力、洛伦兹力三力的大小之比，并指出油滴带何种电荷；
（2）油滴在P点得到的初速度大小：
（3）油滴在第一象限运动的时间。
（1） mg ∶qE ∶f＝1 ∶1 ∶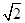
油滴带负电荷 （2）
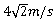（3） 0.828s
题目分析： （1）
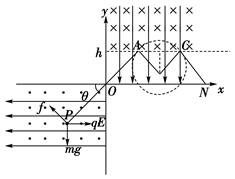
根据受力分析（如图）可知油滴带负电荷 （2分）
设油滴质量为m，由平衡条件得：mg ∶qE ∶f＝1 ∶1 ∶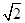 （2分）
（2）由第（1）问得：m＝qE/g （2分）
qvB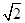＝qE （2分）
解得：v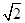＝E/B=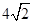
m/s （1分）
（3）进入第一象限，电场力和重力平衡，知油滴先作匀速直线运动，进入y≥h的区域后作匀速圆周运动，路径如图，最后从x轴上的N点离开第一象限 （2分）
由O→A匀速运动的位移为s1＝h/sin45°=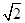h （2分）
其运动时间：t1＝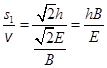
＝0.1s （1分）
由几何关系和圆周运动的周期关系式T＝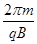
（2分）
知由A→C的圆周运动时间为t2＝0.25T＝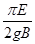
＝0.628s （2分）
由对称性知从C→N的时间t3＝t1 （1分）
在第一象限运动的总时间t＝t1＋t2＋t3＝2×0.1s＋0.628s＝0.828s （1分）