问题
解答题
已知函数f（x）=ax3+bx2+cx-3a（a，b，c∈R且a≠0），当x=-1时，f（x）取到极大值2．
（1）用a分别表示b和c；
（2）当a=l时，求f（x）的极小值；
（3）求a的取值范围．
答案
解：（1）∵函数f（x）=ax3+bx2+cx﹣3a，∴f'（x）=3ax2 +2bx+c．
由题意可得 
，即 
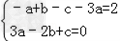，解得 
．
（2）当a=l时，b=2，c=1，函数f（x）=x3 +2x2 +x﹣3，
令f'（x）=3x2 +4x+1=（3x+1）（x+1）=0，可得x=﹣1 x=﹣
．
在（﹣∞，﹣1）、（﹣
，+∞）上，f?（x）＜0，在（﹣1，﹣
）上f'（x）＞0，
故当 x=﹣
时，函数f（x）有极小值为f（﹣
）=
．
（3）由（1）得f'（x）=3ax2+2（a+1）x+2﹣a=3a（x+1）（x﹣
），
令f'（x）=0解得x1=﹣1，x2=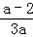
，
∴要使f（x）极大值为f（﹣1）=2，
则 
，或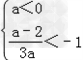 
．
解得 a＞
．