问题
解答题
知函数f(x)=lnx-a2x2+ax(a∈R)。
(1)若函数f(x)在区间(1,+∞)上是单调减函数,求实数a的取值范围;
(2)讨论f(x)的极值。
答案
解:(1):①当a=0时,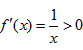 ,
,
∴f(x)在区间(1,+∞)上为增函数,不合题意;
②当a≠0时,要使函数f(x)在区间上(1,+∞)是减函数,只需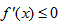 在区间(1,+∞)上恒成立,
在区间(1,+∞)上恒成立,
∵x>0,
∴只要 成立,
成立,
∴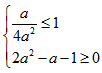
解得 或
或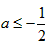 ,
,
综上,实数a的以值范围是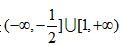 ;
;
(2)函数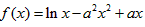 的定义域为(0,+∞),
的定义域为(0,+∞),
∴ ,
,
①当a=0时,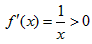 ,
,
∴f(x)的增区间为(0,+∞),此时f(x)无极值;
②当a>0时,令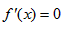 ,得
,得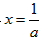 或
或 (舍去),
(舍去),
∴f(x)的增区间为 ,减区间为
,减区间为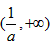 ,
,
所以此时f(x)有极大值为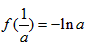 ,无极小值;
,无极小值;
③当a<0时,令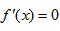 ,得
,得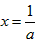 (舍去)或
(舍去)或 ,
,
∴f(x)的增区间为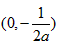 ,减区间为
,减区间为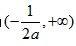 。
。
