问题
解答题
已知函数f(x)=x3+(4﹣a)x2﹣15x+a,a∈R.
(I)若点P(0,﹣2)在函数f(x)的图象上,求a的值和函数f(x)的极小值;
(II)若函数f(x)在(﹣1,1)上是单调递减函数,求a的最大值.
答案
解:(I)∵点P(0,﹣2)在函数f(x)的图象上
∴a=﹣2
∴f(x)=x3+6x2﹣15x﹣2
∴f '(x)=3x2+12x﹣15=3(x﹣1)(x+5)
令f '(x)=0,解得x=﹣5或x=1
令f '(x)<0,解得﹣5<x<1,
∴函数的单调减区间为(﹣5,1)
令f '(x)>0,解得x<﹣5或x>1,
∴函数的单调增区间为(﹣∞,﹣5),(1,+∞)
∴x=1时,函数f(x)取到极小值为f(x)=1+6﹣15﹣2=﹣10
(II)f '(x)=3x2+2(4﹣a)x﹣15要使函数f(x)在(﹣1,1)上是单调递减函数,
则f '(x)≤0在(﹣1,1)上恒成立
∴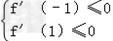
∴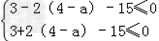
∴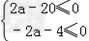
∴﹣2≤a≤10
∴a的最大值为10.
