问题
解答题
已知函数f(x)=x3﹣3ax2+3x+1.
(1)若f(x)在实数集R上单调递增,求实数a的取值范围;
(2)设f(x)在区间(2,3)中至少有一个极值点,求实数a的取值范围.
答案
解:(1)因为f(x)在实数集R上单调递增,
∴f'(x)=3x2﹣6ax+3≥0恒成立
∴△=36(a2﹣1)≤0,
解得:﹣1≤a≤1
(2)f'(x)=3(x2﹣2ax+1)=3[(x﹣a)2+1﹣a2]
当 1﹣a2≥0时,f'(x)≥0,f(x)在R上无极值点,
当 1﹣a2<0时,|a|>1,
令f'(x)=0,易得f(x)有两个极值点 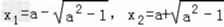
因为f(x)在区间(2,3)中至少有一个极值点,
所以,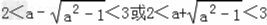
不等式 2<a﹣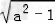 =
=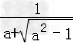 <3,无解,
<3,无解,
解不等式 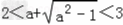 得
得 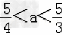 .
.
所以,a的取值范围是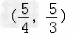

 溶液中通入过量的CO2气体,最终不会出现浑浊的是:( )
溶液中通入过量的CO2气体,最终不会出现浑浊的是:( )