问题
填空题
有四张正面分别标有数字-2,-6,2,6的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中抽取一张,将该卡片上的数字记为a;不放回,再从中抽取一张,将该卡片上的数字记为b,则使关于x的不等式组
|
答案
根据题意列出树状图得:
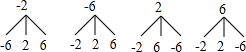
则(a,b)的等可能结果有:(-2,-6),(-2,2),(-2,6),(-6,-2),(-6,2),
(-6,6),(2,-2),(2,6),(2,-6),(6,-2),(6,2),(6,-6)共12种;
,
<x+3x-2 2
①5 2 ax>b②
解①得:x<7,
当a>0,
解②得:x>
,b a
根据不等式组的解集中有且只有3个非负整数解,
则3<x<7时符合要求,
故
=3,b a
即b=6,a=2符合要求,
当a<0,
解②得:x<
,b a
根据不等式组的解集中有且只有3个非负整数解,
则x<3时符合要求,
故
=3,b a
即b=-6,a=-2符合要求,
故所有组合中只有2种情况符合要求,
故使关于x的不等式组
的解集中有且只有3个非负整数解的概率为:
<x+3x-2 2 5 2 ax>b
=2 12
.1 6
故答案为:
.1 6
