问题
解答题
已知在函数f(x)=mx3﹣x的图象上以N(1,n)为切点的切线的倾斜角为 .
(1)求m、n的值;
(2)是否存在最小的正整数k,使得不等式f(x)≤k﹣1995对于x∈[﹣1,3]恒成立?如果存在,请求出最小的正整数k;如果不存在,请说明理由.
答案
解:(1)f'(x)=3mx2﹣1,
依题意,得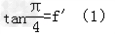 ,
,
即1=3m﹣1,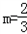
∴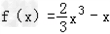 ,把N(1,n)代入,得
,把N(1,n)代入,得
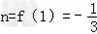 ,
,
∴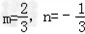
(2)令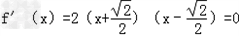 ,则
,则
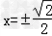 ,
,
当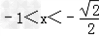 时,f'(x)=2x2﹣1>0,f(x)在此区间为增函数
时,f'(x)=2x2﹣1>0,f(x)在此区间为增函数
当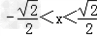 时,f'(x)=2x2﹣1<0,f(x)在此区间为减函数
时,f'(x)=2x2﹣1<0,f(x)在此区间为减函数
当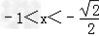 时,f'(x)=2x2﹣1>0,f(x)在此区间为增函数处取得极大值
时,f'(x)=2x2﹣1>0,f(x)在此区间为增函数处取得极大值
又因此,当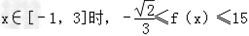 ,
,
要使得不等式f(x)≤k﹣1995对于x∈[﹣1,3]恒成立,则k≥15+1995=2010
所以,存在最小的正整数k=2010,使得不等式f(x)≤k﹣1992对于x∈[﹣1,3]恒成立.

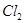 使鲜艳的红色花瓣褪色
使鲜艳的红色花瓣褪色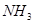 与
与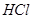 气体接触时有白烟产生
气体接触时有白烟产生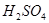 发生钝化
发生钝化