问题
解答题
设函数f(x)=tx2+2t2x+t﹣1(x∈R,t>0).
(I)求f (x)的最小值h(t);
(II)若h(t)<﹣2t+m对t∈(0,2)恒成立,求实数m的取值范围.
答案
解:(I)∵f(x)=t(x+t)2﹣t3+t﹣1(x∈R,t>0),
∴当x=﹣t时,f(x)取最小值f(﹣t)=﹣t2+t﹣1,即h(t)=﹣t3+t﹣1;
(II)令g(t)=h(t)﹣(﹣2t+m)=﹣t3+3t﹣1﹣m,
由g′(t)=﹣3t2+3=0得
t=1,t=﹣1(不合题意,舍去)
当t变化时g′(t)、g(t)的变化情况如下表:
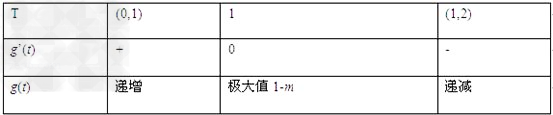
∴g(t)在(0,2)内有最大值g(1)=1﹣m
h(t)<﹣2t+m在(0,2)内恒成立等价于g(t)<0在(0,2)内恒成立,
即等价于1﹣m<0
所以m的取值范围为m>1.
