解：（1）由题意可得：

函数f（x）=x³+bx²+cx+d的导数为：f ’（x）=3x²+2bx+c

因为函数f（x）=x³+bx²+cx+d有两个极值点x₁=1，x₂=2

所以3x²+2bx+c=0的两个根为x₁=1，x₂=2

所以2b+c+3=0，并且4b+c+12=0，解得：b=﹣，c=6．

（2）设切点为（x₀，y₀），由（1）可得：f ’（x）=3x²﹣9x+6，因为直线y=6x+1与曲线y=f（x）相切于P点，所以f ’（x₀）=6，即x₀=3或者x₀=0，当x₀=3时，y₀=19，所以函数y=f（x）的解析式为f（x）=x³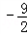x²+6x+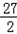．当x₀=0时，y₀=1，所以函数y=f（x）的解析式为f（x）=x³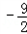x²+6x+1．

（3）由题意可得：f（x）=x³x²+6x+1，并且P（0，1），

设切点的坐标为（x₁，y₁），

所以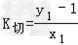==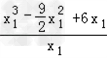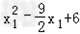…①．

又因为f ’（x）=3x²﹣9x+6，所以K切=3x₁²﹣9x₁+6…②，由①②可得：，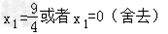

所以切点为（，），

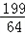所以，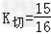

所以切线方程为15x﹣16y+16=0．

所以过P点和y=f（x）相切于一异于P点的直线方程为

15x﹣16y+16=0．