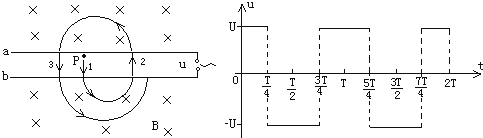
在D型盒回旋加速度器中,高频交变电压(假设为右图所示的方形波)加在a板和b板间,带电粒子在a、b间的电场中加速,电压大小为U=800V,在匀强磁场中做匀速圆周运动,磁感应强度大小B=0.628T,a板与b板间的距离d=0.1mm,被加速的粒子为质子,质子的质量约为m=1.6×10-27kg,电荷量为q=1.6×10-19C.t=0时刻,静止的质子从靠近a板的P点开始第1次加速,t=T/2时刻恰好第2次开始加速,t=T时刻恰好第3次开始加速,…,每隔半个周期加速一次.(每一次加速的时间与周期相比可以忽略,不考虑相对论中因速度大而引起质量变化的因素)
(1)求交变电压的周期T.
(2)求第900次加速结束时,质子的速度多大?
(3)虽然每一次的加速时间可以忽略,但随着加速次数的增多,在电场中运动的时间累积起来就不能忽略了.求第n次完整的加速过程结束时质子在ab间电场中加速运动的总时间t(用相关物理量的字母符号如U、d…表示,不需代入数值)
(1)交变电压的周期T恰等于质子在磁场中圆周运动的周期,即
T=
①2πm qB
代入得T=
s=1.0×10-7s ②2×3.14×1.6×10-27 1.6×10-19×0.628
(2)对900次加速的整个过程应用动能定理
NqU=
mV2③1 2
得V=
=2NqU m
m/s=1.2×107m/s ④2×900×1.6×10-19×800 1.6×10-27
(3)每次加速都是一个匀加速过程,而在磁场中速率不变,所以可以把n次加速的过程看成一个一次性加速过程.
对整个应用牛顿第二定很和运动学公式
=ma⑤qU d
得a=
⑥qU md
nd=
(1 2
)t加2⑦qU md
得t加=d
⑧2nm qU
答:(1)则交变电压的周期1.0×10-7s.
(2)则第900次加速结束时,质子的速度1.2×107m/s;
(3)虽然每一次的加速时间可以忽略,但随着加速次数的增多,在电场中运动的时间累积起来就不能忽略了.则第n次完整的加速过程结束时质子在ab间电场中加速运动的总时间d
.2nm qU
