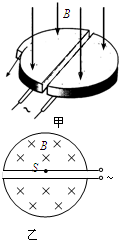
在高能物理研究中,粒子回旋加速器起着重要作用,如图甲为它的示意图.它由两个铝制D型金属扁盒组成,两个D形盒正中间开有一条窄缝.两个D型盒处在匀强磁场中并接有高频交变电压.图乙为俯视图,在D型盒上半面中心S处有一正离子源,它发出的正离子,经狭缝电压加速后,进入D型盒中.在磁场力的作用下运动半周,再经狭缝电压加速.如此周而复始,最后到达D型盒的边缘,获得最大速度,由导出装置导出.已知正离子的电荷量为q,质量为m,加速时电极间电压大小为U,磁场的磁感应强度为B,D型盒的半径为R.每次加速的时间很短,可以忽略.正离子从离子源出发时的初速度为零.
(1)为了使正离子每经过窄缝都被加速,求交变电压的频率;
(2)求离子能获得的最大动能;
(3)求离子第1次与第n次在下半盒中运动的轨道半径之比.
(1)使正离子每经过窄缝都被加速,交变电压的频率应等于离子做圆周运动的频率,正离子在磁场中做匀速圆周运动,
由洛伦兹力提供向心力Bqv=m
又T=v2 r
解得T=2πr v
所以f=2πm qB qB 2πm
(2)当离子从D盒边缘离开时速度最大,此时离子做圆周运动的半径为D盒的半径有vm=qBr m
离子获得的最大动能为E=1 2
=mv 2m q2B2R2 2m
(3)离子从S点经电场加速1次后,以速度v1第1次进入下半盒,由动能定理Uq=1 2
得 v1=mv 21 2Uq m
又r1=
=mv1 qB m qB 2qU m
离子从S点经电场加速3次后,以速度v3第2次进入下半盒3Uq=1 2 mv 23
解得v3=
,r2=3×2Uq m
=mv3 qB m qB 3×2qU m
…离子经电场加速(2n-1)次后,第n次进入磁场 同理可得rn=m qB (2n-1)×2qU m
所以
=r1 rn 1 2n-1
答:(1)为了使正离子每经过窄缝都被加速,交变电压的频率为
;qB 2πm
(2)离子能获得的最大动能为
;q2B2R2 2m
(3)离子第1次与第n次在下半盒中运动的轨道半径之比为
=r1 rn
.1 2n-1
