神奇的黑洞是近代引力理论所预言的一种特殊天体，探寻黑洞的方案之一是观测双星系统的运动规律，天文学家观测河外星系大麦哲伦星云时，发现了LMCX-3双星系统，它由可见星A和不可见的暗星B构成．将两颗星视为质点，不考虑其他天体的影响，星A、B围绕二者连线上的O点做匀速圆周运动，它们之间的距离保持不变，如图所示，引力常量为G，由观测能够得到可见星A的速率v和运行周期T。
(1)可见星A所受暗星B的引力FA可等效为位于O点处质量为m'的星体（视为质点）对它的引力，设星A和星B的质量分别为m1，m2，试求m'.（用m1，m2表示）
(2)求暗星B的质量m2与可见星A的速率v、运行周期 T和质量m1之间的关系式．
(3)恒星演化到末期，如果其质量大于太阳质量ms的2倍，它将有可能成为黑洞．若可见星A的速率v=2.7×105m/s，运行周期T=4.7π×104 s，质量m1=6ms，试通过估算来判断暗星B有可能是黑洞吗？ (G=6.67×10-11N.m2/kg2，ms=2.0×1030 kg)
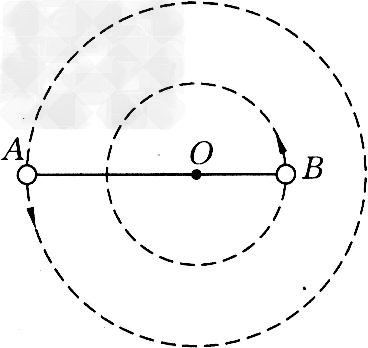
解：(1)设A，B两颗星的轨道半径分别为r1，r2，由题意知，A、B两颗星做匀速圆周运动的角速度相同，设其为ω
由牛顿运动定律，有FA= m1ω2r1，FB=m2ω2r2，FA= FB
设A，B两颗星之间的距离为r，又r=r1+r2
由上述各式得r=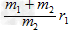
①
由万有引力定律，有FA=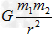
将①代入得FA=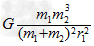
令FA=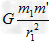
，比较可得m'=
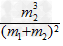②
(2)由牛顿第二定律，有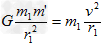
③
又可见星A的轨道半径r1=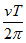
④
由②③④式解得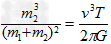
⑤
(3)将m1=6ms代入⑤式，得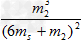
=
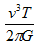
代入数据得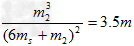
⑥
设m2=nms (n>0)，将其代入⑥式，得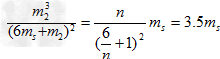
⑦
可见，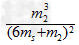
的值随n的增大而增大，试令n=2，得
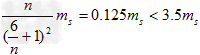⑧
若使⑦式成立，则n必大于2，即暗星B的质量m2必大于2ms，由此得出结论：暗星B有可能是黑洞