问题
计算题
如图,在x轴下方有匀强磁场,磁感应强度大小为B,方向垂直于xy平面向外。P是y轴上距原点为h的一点,N0为x轴上距原点为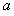 的一点。A是一块平行于x轴的挡板,与x轴的距离为
的一点。A是一块平行于x轴的挡板,与x轴的距离为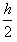 ,A的中点在y轴上,长度略小于
,A的中点在y轴上,长度略小于 。带电粒子与挡板碰撞前后,x方向的分速度不变,y方向的分速度反向、大小不变。质量为m,电荷量为q(q>0)的粒子从P点瞄准N0点入射,最后又通过P点。不计重力。求粒子入射速度的所有可能值。
。带电粒子与挡板碰撞前后,x方向的分速度不变,y方向的分速度反向、大小不变。质量为m,电荷量为q(q>0)的粒子从P点瞄准N0点入射,最后又通过P点。不计重力。求粒子入射速度的所有可能值。

答案
解:
设粒子的入射速度为v,第一次射出磁场的点为N0′,与板碰掩后再次进入磁场的位置为N1。粒子在磁场中运动的半径为R。得R= ①
①
粒子速率不变,每次进入磁场与射子磁场位置间距离x1保持不变,x1=N0′N0=2Rsinθ ②
粒子射出磁场与下一次进入磁场位置间的距离x2始终不变,与N0′N1相等。由图可以看出x1=a ③
设粒子最终离开磁场时,与挡板碰碰n次(n =0,l,2…)。若粒子能回到P点,由对称性,粒子的出射点的x坐标标应为-a,即(n+1)x1-nx2=2a ④
由③④式得:x1=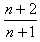 a ⑤
a ⑤
若粒子与挡板发生碰撞,有x1-x2>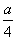 ⑥
⑥
联立③④⑥式得n < 3 ⑦
联立①②⑤式得:v= ·
·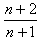 a ⑧
a ⑧
式中sinθ =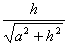 ,代入⑧式得
,代入⑧式得
v0= ,n=0
,n=0
v1=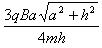 ,n=1
,n=1
v2=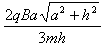 ,n=2
,n=2
