如图所示,在空间有匀强磁场,磁感应强度的方向垂直纸面向里,大小为B,光滑绝缘空心细管MN的长度为h,管内M端有一质量为m、带正电q的小球P,开始时小球P相对管静止,管带着小球P沿垂直于管长度方向的恒定速度u向右运动。设重力及其它阻力均可忽略不计。求:
(1)当小球P相对管上升的速度为v时,小球上升的加速度多大?
(2)小球P从管的另一端N离开管口后,在磁场中作圆周运动的半径R多大?
(3)小球P在从管的M端到N端的过程中,管壁对小球做的功是多少?
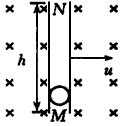
解:(1)设此时小球的合速度大小为v合,方向与u的夹角为θ有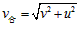 ①
①
cosθ=u/v合=u/ 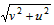 ②
②
此时粒子受到的洛伦兹力f和管壁的弹力N如图所示,
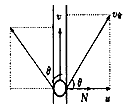
由牛顿第二定律可求此时小球上升的加速度为:a=fcosθ=qv合Bcosθ/m③
联立①②③解得:a=quB/m
(2)由上问可知,小球上升加速度只与小球的水平速度u有关,故小球在竖直方向上做匀加速运动。
设小球离开N端管口时的竖直分速度为vy,由运动学公式得
此时小球的合速度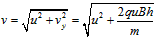
故小球运动的半径为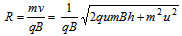
(3)因洛伦兹力对小球做的功为零,由动能定理得管壁对小球做的功为:W= mv2/2-mu2/2=quBh。
