问题
计算题
如图，在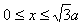
区域内存在与xy平面垂直的匀强磁场，磁感应强度的大小为B。在t=0时刻，一位于坐标原点的粒子源在xy平面内发射出大量同种带电粒子，所有粒子的初速度大小相同，方向与y轴正方向的夹角分布在0～180°范围内。已知沿y轴正方向发射的粒子在t=t0时刻刚好从磁场边界上
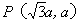点离开磁场。求：
（1）粒子在磁场中做圆周运动的半径R及粒子的比荷q/m；
（2）此时刻仍在磁场中的粒子的初速度方向与y轴正方向夹角的取值范围；
（3）从粒子发射到全部粒子离开磁场所用的时间。
答案
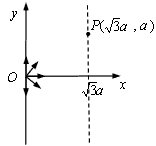
解：（1）初速度沿y轴的正方向的粒子在磁场中的运动轨迹如图1所示：
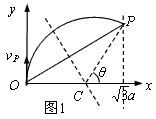
粒子沿y轴的正方向进入磁场，从P点经过，作OP的垂直平分线与x轴的交点为圆心C，在直角三角形中有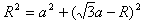
解得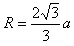
，
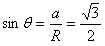
则粒子做圆周运动的的圆心角为120°，周期为T=3t0
粒子做圆周运动的向心力由洛仑兹力提供，根据牛顿第二定律得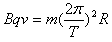
，
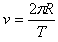
化简得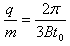
（2）依题意，同一时刻仍在磁场内的粒子到O点距离相同。在t0时刻仍在磁场内的粒子应位于以O为圆心、OP为半径的弧MN上，如图2所示：
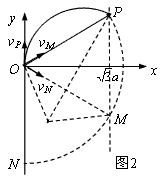
设此时位于P、M、N三点的粒子的初速度分别为vP、vM、vN。由对称性可知：vP与OP、vM与OM、vN与ON的夹角均为60°，设vM、vN与y轴的夹角分别为θM、θN，由几何关系有：θM=60°，θN=120°
对于所有此时刻仍在磁场内的粒子，其初速度与y轴的正方向的夹角范围应满足60°≤θ≤120°
（3）在磁场中运动时间最长的粒子的轨迹应该与磁场的右边界相切，其轨迹如图3所示：
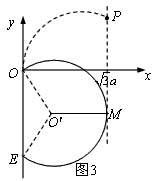
在三角形OO'E中，两个相等的腰为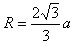
而它的高是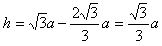
半径O'E与y轴的的夹角是30°，这种粒子的圆心角是240°，所用时间为2t0
所以从粒子发射到全部离开所用时间为2t0