解：（1）∵f（x）=x²+bx+c为偶函数，

故f（﹣x）=f（x）

即有（﹣x）²+b（﹣x）+c=x²+bx+c

解得b=0又曲线y=f（x）过点（2，5），

得2²+c=5，有c=1

∵g（x）=（x+a）f（x）=x³+ax²+x+a

从而g'（x）=3x²+2ax+1，

∵曲线y=g（x）有斜率为0的切线，

故有g'（x）=0有实数解．即3x²+2ax+1=0有实数解．

此时有△=4a²﹣12≥0

解得a∈（﹣∞，﹣]∪[，+∞）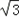

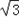所以实数a的取值范围：a∈（﹣∞，﹣]∪[，+∞）；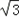

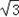（2）因x=﹣1时函数y=g（x）取得极值，

故有g'（﹣1）=0即3﹣2a+1=0，

解得a=2

又g'（x）=3x²+4x+1=（3x+1）（x+1）

令g'（x）=0，得=﹣1，x₂=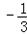

当x∈（﹣∞，﹣1）时，g'（x）＞0，故g（x）在（﹣∞，﹣1）上为增函数

当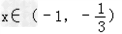时，g'（x）＜0，故g（x）在（﹣1，﹣）上为减函数

当x∈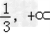（﹣）时，g'（x）＞0，故g（x）在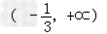上为增函数．