问题
问答题
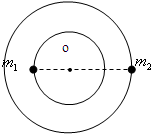
两个靠得很近的天体,离其它天体非常遥远,它们以其连线上某一点O为圆心各自做匀速圆周运动,两者的距离保持不变,科学家把这样的两个天体称为“双星”,如图所示.已知双星的质量为m1和m2,它们之间的距离为L.求双星运行轨道半径r1和r2,以及运行的周期T.
答案
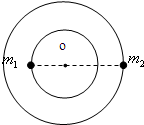
如图,
设双星中质量为m1的天体轨道半径为r1,质量为m1的天体轨道半径为r2
据万有引力定律和牛顿第二定律,得:
G
=m1ω2r1①m1m2 L2
G
=m2ω2r2②m1m2 L2
r1+r2=L③
由①②③联立解得:
r1=m2L m1+m2
r2=m1L m1+m2
再由:G
=m1m1m2 L2
r1得4π2 T2
运行的周期T=2πLL G(m1+m2)
答:双星运行轨道半径分别为:r1=
,r2=m2L m1+m2
,周期为2πLm1L m1+m2 L G(m1+m2)
