问题
计算题
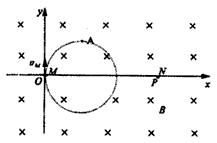
如图所示,在坐标系内有垂直所在平面的范围足够大的匀速磁场,磁感应强度为B。某时刻有两个粒子M、N分别从坐标原点O及轴上的P点开始运动。M粒子带电量为q,质量为m,初速度方向沿y轴正方向,速度大小为VM。运动轨迹如图所示。N粒子带电量为q,质量为m/2,初速度方向是在xoy平面内的所有可能的方向,P点到O点距离是M粒子轨道半径的3倍,两粒子所受的重力不计。
(1)M粒子带的是正电还是负电运动的轨道半径RM是多少?
(2)若两个粒子相遇的位置在(RM,RM)的A点,则N粒子速度VN是多大?
(3)N粒子的速度VN有一临界值V,当VN<V时,两个粒子不可能相遇,求临界值v的大小。
答案
解:(1)由左手定则知,M粒子带负电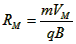
(2)由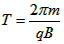 知
知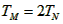 , M粒子由O点运动到A点的时间为
, M粒子由O点运动到A点的时间为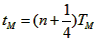 ,
,
N粒子由P点运动到A点的时间为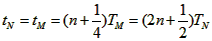
可知,AN长度为粒子N做圆周运动的直径,由几何关系有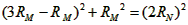
解得: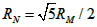
又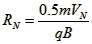
可得: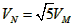
(3)如图所示,

假设两粒子相遇在Q点,由几何关系有PQ=2RNsinθ
由正弦定理有PQ/sinα=RM/sinβ
即2RNsinθ/sin(π-θ)=RM/sinβ
得2RN=RM/sinβ,VN=VM/sinβ
又由于
得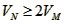 ,即:v=2VM
,即:v=2VM
