问题
计算题
如图，在O≤x≤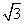
a区域内存在与xy平面垂直的匀强磁场，磁感应强度的大小为B。在t=0时刻，一位于坐标原点的粒子源在xy平面内发射出大量同种带电粒子，所有粒子的初速度大小相同，方向与y轴正方向的夹角分布在0~ 180°范围内。已知沿y轴正方向发射的粒子在t=t0时刻刚好从磁场边界上P（
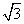a，a）点离开磁场。求：
（1）粒子在磁场中做圆周运动的半径R及粒子的比荷q/m；
（2）此时刻仍在磁场中的粒子的初速度方向与y轴正方向夹角的取值范围；
（3）从粒子发射到全部粒子离开磁场所用的时间。
答案
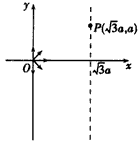
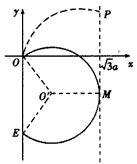
解：（1）初速度与y轴正方向平行的粒子在磁场中的运动轨迹如下图中的弧OP所示，其圆心为C
由题给条件可以得出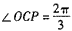
①
此粒子飞出磁场所用时间为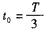
②
式中T为粒子做圆周运动的周期。设粒子运动速度的大小为v，半径为R，由几何关系可得
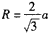③
由洛伦兹力公式和牛顿第二定律有
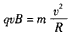④
⑤
联立②③④⑤式，得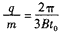
（2）依题意，同一时刻仍在磁场内的粒子到O点距离相同。在t0时刻仍在磁场中的粒子应位于以O点为圆心、OP为半径的弧MN上，如图所示
设此时位于P、M、N三点的粒子的初速度分别为vp、vM、vN，由对称性可知vp与OP、vM与OM、vN与ON的夹角均为π/3。设vM、vM与y轴正向的夹角分别为θM、θN，由几何关系有
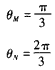
对于所有此时仍在磁场中的粒子，其初速度与y轴正方向所成的夹角θ应满足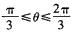
（3）在磁场中飞行时间最长的粒子的运动轨迹应与磁场右边界相切，其轨迹如上图所示。由几何关系可知，弧OM=弧OP
由对称性可知，弧ME=弧OP
从粒子发射到全部粒子飞出磁场所用的时间tm=2t0