问题
解答题
已知实数a＜0，函数f（x）=ax（x﹣1）2+a+1（x∈R）．
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）若f（x）有极大值﹣7，求实数a的值．
答案
解：（Ⅰ）∵f（x）=ax（x﹣1）2+a+1，
∴f′（x）=a（3x2﹣4x+1）．
令f′（x）=0，
∵a＜0，∴3x2﹣4x+1=0，即（3x﹣1）（x﹣1）=0，
∴x=
或x=1
当x∈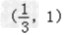
时，f′（x）＞0，f（x）的单调递增区间为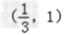 
当x∈（﹣∞， 
）或x∈（1，+∞）时，f′（x）＜0，
f（x）的单调递减区间为（﹣∞，
），（1，+∞）．
（Ⅱ）∵x∈（﹣∞，
）时，f′（x）＜0，
x∈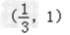
时，f′（x）＞0，
x∈（1，+∞）时，f′（x）＜0，
∴f（x）在x=1处取得极大值﹣7．即a+1=﹣7，
解得a=﹣8