问题
计算题
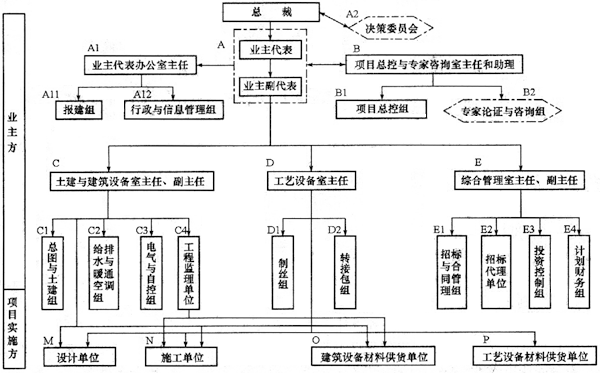
如图,在直角坐标系xoy中,点M(0,1)处不断向+y方向发射出大量质量为m、带电量为-q的粒子,粒子的初速度大小广泛分布于零到v0之间。已知这些粒子此后所经磁场的磁感应强度大小为B,方向垂直于纸面向里,所有粒子都沿+x方向经过b区域,都沿-y的方向通过点N(3,0)。
(1)通过计算,求出符合要求的磁场范围的最小面积;
(2)若其中速度为k1v0和k2v0的两个粒子同时到达N点(1>k1>k2>0),求二者发射的时间差。
答案
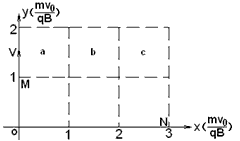
解:(1)在a区域,设任一速度为v的粒子偏转90°后从(x,y)离开磁场,由几何关系有
 ,
, ,得
,得
上式与R无关,说明磁场右边界是一条直线
左边界是速度为v0的粒子的轨迹: ,
,
此后粒子均沿+x方向穿过b区域,进入c区域,由对称性知,其磁场区域如图
磁场的面积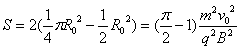
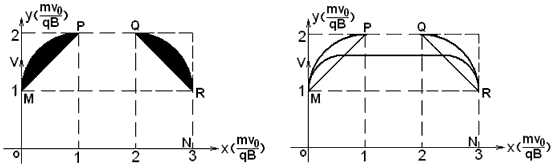
(2)如图所示,速度为k1v0的粒子在a区域磁场的时间为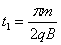
两个阶段的直线运动的时间共为
在c区域磁场的时间为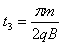
所以这两个粒子的发射时间差只与t2有关
速度为k2v0的粒子在直线运动阶段的时间为