问题
计算题
如图所示,有三个宽度均为d的区域I、Ⅱ、Ⅲ;在区域I和Ⅲ内分别为方向垂直于纸面向外和向里的匀强磁场(虚线为磁场边界面,并不表示障碍物),区域I磁感应强度大小为B,某种带正电的粒子,从孔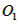 以大小不同的速度沿图示与夹角的方向进入磁场(不计重力),已知速度为
以大小不同的速度沿图示与夹角的方向进入磁场(不计重力),已知速度为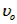 和
和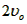 时,粒子在区域I内的运动时间相同,均为
时,粒子在区域I内的运动时间相同,均为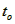 ;速度为
;速度为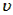 时粒子在区域I内的运时间为
时粒子在区域I内的运时间为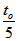 。求:
。求:
(1)粒子的比荷 和区域I的宽度
和区域I的宽度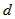 ;
;
(2)若区域Ⅲ磁感应强度大小也为B,速度为v的粒子打到边界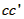 上的位置P点到
上的位置P点到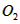 点的距离;
点的距离;
(3) 若在图中区域Ⅱ中O1O2上方加竖直向下的匀强电场,O1O2下方对称加竖直向上的匀强电场,场强大小相等,使速度为v的粒子每次均垂直穿过I、Ⅱ、Ⅲ区域的边界面并能回到O1点,则所加电场场强和区域Ⅲ磁感应强度大小为多大?并求出粒子在场中运动的总时间。

答案
解:(1)由题
得
当速度为v时,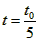 ,圆心角
,圆心角
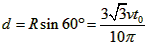
(2)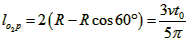
(3)
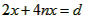 ,(n=0、1、2、3…… )
,(n=0、1、2、3…… )
得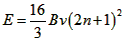 ,
,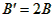
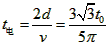
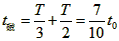
综上 。
。
