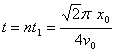问题
计算题
在实验室中，需要控制某些带电粒子在某区域内的滞留时间，以达到预想的实验效果。现设想在xOy的纸面内存在以下的匀强磁场区域，在O点到P点区域的x轴上方，磁感应强度为B，方向垂直纸面向外，在x轴下方，磁感应强度大小也为B，方向垂直纸面向里，OP两点距离为x0（如图所示）。现在原点O处以恒定速度v0不断地向第一象限内发射氘核粒子。
（1）设粒子以与x轴成45°角从O点射出， 第一次与x轴相交于A点，第n次与x轴交于P点，求氘核粒子的比荷
（用已知量B、x0、v0、n表示），并求OA段粒子运动轨迹的弧长（用已知量x0、v0、n表示）。
（2）求粒子从O点到A点所经历时间t1和从O点到P点所经历时间t（用已知量x0、v0、n表示）。
答案
解：（1）氘核粒子在匀强磁场中做匀速圆周运动，由牛顿第二定律得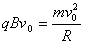
解得粒子运动的半径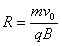
由几何关系知，粒子从A点到O点的弦长为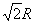
，由题意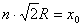
解得氘核粒子的比荷：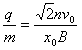
由几何关系得，OA段粒子运动轨迹的弧长：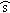
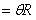
圆心角：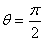
由以上各式解得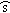
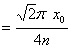
（2）粒子从O点到A点所经历时间：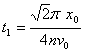
从O点到P点所经历时间