如图所示,空间有一个垂直于xOy平面向里的有界匀强磁场,磁场的边界分别是y=1m、y=0、x=1.5 m、x=-1.5 m。一束带正电的粒子垂直于磁场从O点沿y轴正方向以不同大小的速度射入磁场,已知带电粒子的 质量m=1×10-6 kg,带电荷量q=2×10-4 C,磁感应强度B=0.5 T,不计带电粒子的重力和粒子间的相互作用。试求:
(1)若某个粒子经过坐标(-1.5,0.5 )处,则该粒子射入磁场的速度和在磁场中运动的时间分别为多少?
)处,则该粒子射入磁场的速度和在磁场中运动的时间分别为多少?
(2)若从O点射入粒子的速度均大于200 m/s,则求粒子从磁场上边界射出的范围。
(3)若只改变磁场区域的上边界y的值,使粒子无论以多大的速度从O点射入磁场后都不会从磁场的左边界射出,求磁场上边界y的值。

解:(1)粒子在匀强磁场中运动轨迹如图(a)所示,由几何关系可得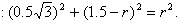

由牛顿第二定律可知: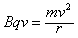
解得:r=1 m,v=100 m/s
又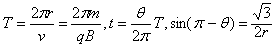
解得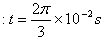
(2)粒子的速度均大于200 m/s,则由(1)可知粒子必从上边界射出磁场,速度为200 m/s时,粒子的运动轨迹示意图如图(b)所示,由Bqv2=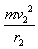
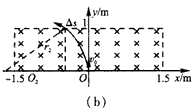
又几何关系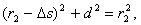
解得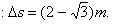
即粒子从磁场上边界y轴的左侧射出且到y轴的距离s满足0<s≤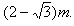
(3)不从左侧边界射出,即从磁场的上边界射出或下边界射出,其临界轨迹为恰好与上边界相切且又从下边界射出,粒子运动轨迹如图(c)所示,故左边界到y轴的距离正好是上边界到x轴距离的两倍

即满足题意的上边界坐标y≤0.75 m
